Postdoctoral position in Network Science - Machine Learning
The Mapping Complexity Lab of Prof. M. Ángeles Serrano and Prof. M. Boguñá is opening a call to hire a postdoctoral researcher in the Department of Condensed Matter Physics at the University of Barcelona.

Requirements:
A PhD in physics, computer science, computer/electronic engineering, mathematics, or other related disciplines.
Interest in interdisciplinary research, curiosity about AI and networks, high motivation to learn, an open-minded and collaborative spirit.
Excellent software development skills.
Excellent communication skills, and proficient in the English language, both written and spoken.

Offer:
The successful applicant will work with Prof. M. Ángeles Serrano and Prof. Marián Boguñá at the interface between Network Science and Machine Learning. The goal is to merge the best of the two worlds to produce a new generation of models and methods for the classification and prediction of complex networks. We offer a 2-year position (1+1) with a competitive salary.

Application process:
Interested applicants are requested to submit a Curriculum Vitae including relevant publications and the name and contact details of 2 referees.
We promote diversity and equal opportunities, minorities in science are encouraged to apply.
Queries about this position should be sent to marian.serrano@ub.edu or marian.boguna@ub.edu

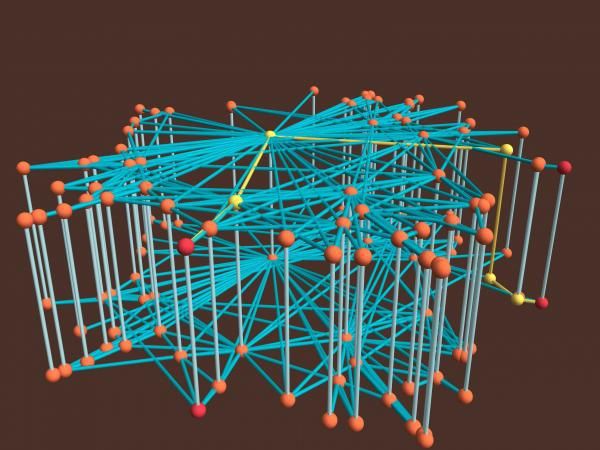
Almagro, P.; Boguñá, M.; Serrano, M. A. «Detecting the ultra low dimensionality of real networks». Nature Communications 13, 6096 (2022)

https://www.nature.com/articles/s43588-022-00362-6

https://www.ub.edu/web/ub/en/menu_eines/noticies/2022/10/046.html

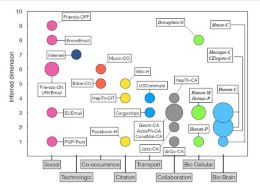
Recent advances in network science include the discovery that complex networks have a hidden geometry and that this geometry is hyperbolic. Studying complex networks through the lens of their effective hyperbolic geometry has led to valuable insights on the organization of a variety of complex systems ranging from the Internet to the metabolism of E. coli and humans. This methodology can also be used to infer high-quality maps of connectomes, where brain regions are given coordinates in hyperbolic space such that the closer they are the more likely that they are connected. Even if Euclidean space is typically assumed as the natural geometry of the brain, distances in hyperbolic space offer a more accurate interpretation of the structure of connectomes, which suggests a new perspective for the mapping of the organization of the brain’s neuroanatomical regions.

In humans, this approach has been able to explain the multiscale organization of connectomes in healthy subjects at five anatomical resolutions. Zoomed-out connectivity maps remain self-similar and our geometric network model, where distances are not Euclidean but hyperbolic, predicts the observations by application of a renormalization protocol. Our results prove that the same principles organize brain con-nectivity at different scales and lead to efficient decentralized communication.

If you want to see more:

Geometric renormalization unravels self-similarity of the multiscale human connectome

PNAS 117 20244-20253 (2020)    

Navigable maps of structural brain networks across species

PLoS Computational Biology 16 e1007584 (2020)

Scaling up real networks by geometric branching growth

PNAS May 25, 2021 118 (21) e2018994118; https://doi.org/10.1073/pnas.2018994118  

Branching processes underpin the complex evolution of many real systems. However, network models typically describe network growth in terms of a sequential addition of nodes. Here, we measured the evolution of real networks—journal citations and international trade—over a 100-y period and found that they grow in a self-similar way that preserves their structural features over time. This observation can be explained by a geometric branching growth model that generates a multiscale unfolding of the network by using a combination of branching growth and a hidden metric space approach. Our model enables multiple practical applications, including the detection of optimal network size for maximal response to an external influence and a finite-size scaling analysis of critical behavior.                                                                                                                                                     

Multiscale unfolding of real networks by geometric renormalization

Nature Physics doi:10.1038/s41567-018-0072-5 (2018)

Symmetries in physical theories denote invariance under some transformation, such as self-similarity under a change of scale. The renormalization group provides a powerful framework to study these symmetries, leading to a better understanding of the universal properties of phase transitions. However, the small-world property of complex networks complicates application of the renormalization group by introducing correlations between coexisting scales. Here, we provide a framework for the investigation of complex networks at different resolutions. The approach is based on geometric representations, which have been shown to sustain network navigability and to reveal the mechanisms that govern network structure and evolution. We define a geometric renormalization group for networks by embedding them into an underlying hidden metric space. We find that real scale-free networks show geometric scaling under this renormalization group transformation. We unfold the networks in a self-similar multilayer shell that distinguishes the coexisting scales and their interactions. This in turn offers a basis for exploring critical phenomena and universality in complex networks. It also affords us immediate practical applications, including high-fidelity smaller-scale replicas of large networks and a multiscale navigation protocol in hyperbolic space, which betters those on single layers.

Mercator is a new embedding tool to create maps of networks in the hyperbolic plane. Download it now from GitHub or acces our NETS2MAPS platform!

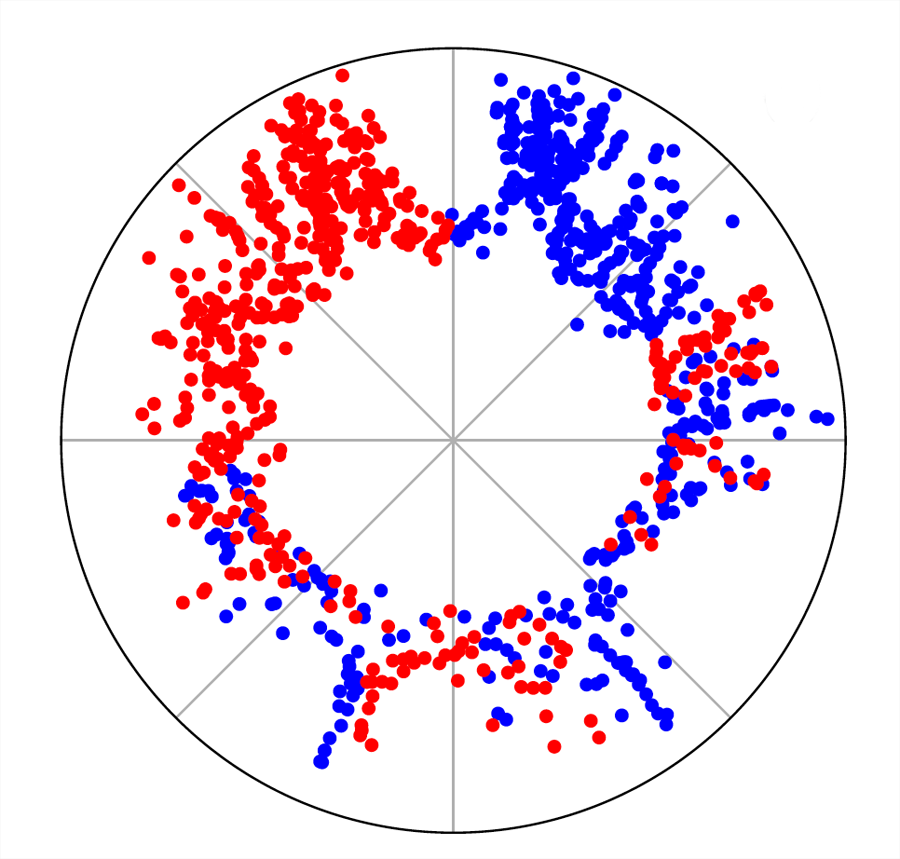
Mercator is a reliable embedding method to map real complex networks into their hyperbolic latent geometry. The method assumes that the structure of networks is well described by the PopularityxSimilarity S1/H2 static geometric network model, which can accommodate arbitrary degree distributions and reproduces many pivotal properties of real networks, including self-similarity patterns. The algorithm mixes machine learning and maximum likelihood approaches to infer the coordinates of the nodes in the underlying hyperbolic disk with the best matching between the observed network topology and the geometric model. In its fast mode, Mercator uses a model-adjusted machine learning technique performing dimensional reduction to produce a fast and accurate map, whose quality already outperform other embedding algorithms in the literature. In the refined Mercator mode, the fast-mode embedding result is taken as an initial condition in a Maximum Likelihood estimation, which significantly improves the quality of the final embedding. Apart from its accuracy as an embedding tool, Mercator has the clear advantage of systematically inferring not only node orderings, or angular positions, but also the hidden degrees and global model parameters, and has the ability to embed networks with arbitrary degree distributions. Overall, our results suggest that mixing machine learning and maximum likelihood techniques in a model-dependent framework can boost the meaningful mapping of complex networks.

Postdoctoral Position in Mapping Big Data Systems  

Applications are invited for a Postdoctoral fellowship at the University of Barcelona to work with Prof. M. Ángeles Serrano and Prof. Marián Boguñá at the Department of Condensed Matter Physics and UB Institute of Complex Systems (UBICS). The position is funded by a "Fundación BBVA" grant.

This is a postdoctoral position with a salary of €29,700 per year (before taxes) for one year renewable until june 2020. There will be additional support for conference travels.  

Topic  

The discovery and understanding of the hidden geometry of complex networks have become fundamental problems within Network Science giving place to the field of Network Geometry. The research will focus on mixing of machine learning and statistical techniques for an efficient embedding of very large networks in hidden metric spaces to produce meaningful maps. We will create an online platform to host an atlas of network maps, and where scientists and interested people can produce theirs.  

Essential Skills  

• A PhD in Physics, Computer Science, Computer/Electronic Engineering, or other relevant discipline is expected.
• Excellent software development skills - Expertise in complex networks
• Excellent communication skills, verbal and written (English) 

Informal queries about this position should be sent to marian.serrano@ub.edu  

Application process  

Interested applicants are requested to submit a Curriculum Vitae including relevant publications and the name and contact details of 2 referees. Additionally, a one page cover letter explaining your interest in this specific position could be included.

Submissions should be sent by email with subject “MBDS Application” to marian.serrano@ub.edu.
Interviews will be carried out as soon as suitable candidates are identified.
To successful candidate is expected to start in September  2018, or before (if possible).

Metabolic plasticity in synthetic lethal mutants: viability at higher cost

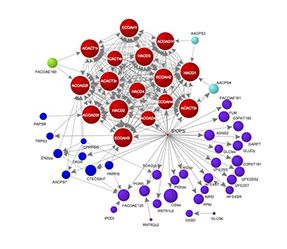
The most frequent form of pairwise synthetic lethality (SL) in metabolic networks is known as plasticity synthetic lethality. It occurs when the simultaneous inhibition of paired functional and silent metabolic reactions or genes is lethal, while the default of the functional partner is backed up by the activation of the silent one. Using computational techniques on bacterial genome-scale metabolic reconstructions, we found that the failure of the functional partner triggers a critical reorganization of fluxes to ensure viability in the mutant which not only affects the SL pair but a significant fraction of other interconnected reactions, forming what we call a SL cluster. Interestingly, SL clusters show a strong entanglement both in terms of reactions and genes. This strong overlap mitigates the acquired vulnerabilities and increased structural and functional costs that pay for the robustness provided by essential plasticity. Finally, the participation of coessential reactions and genes in different SL clusters is very heterogeneous and those at the intersection of many SL clusters could serve as supertargets for more efficient drug action in the treatment of complex diseases and to elucidate improved strategies directed to reduce undesired resistance to chemicals in pathogens.

Rethinking distance in international trade. World Trade Atlas 1870-2013 

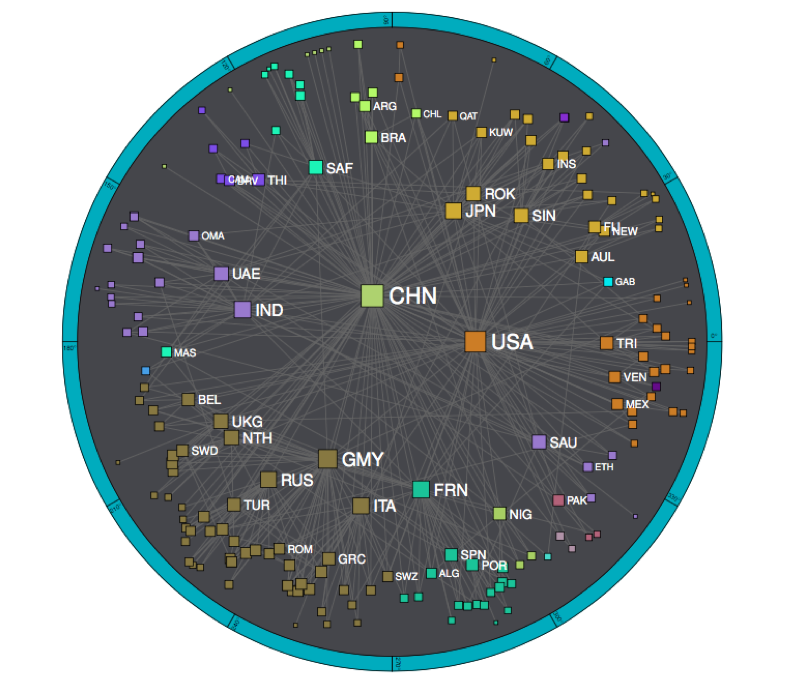
The World Trade Atlas 1870-2013 is a collection of annual World Trade Maps where distance integrates the different dimensions affecting international trade beyond geography. The Atlas informs us about the long-run evolution of the international trade system and shows that, in terms of trade, the world is not flat, it is hyperbolic. The departure from flatness has been increasing since World War I, meaning that differences in trade distances are growing and becoming more hierarchical.Small economies are moving away from the rest of the world, except for their trade with the big economies, while big economies are increasing their chance of getting world-wide connected. At the same time, Preferential Trade Arrangements are not in perfect agreement to natural communities on trade space and have not necessarily effected an internal reduction of trade barriers. We discuss an interpretation in terms of globalization, hierarchicalization, and localization, three forces acting simultaneously to shape the international trade system. Watch the evolution of world trade with this interactive video tool World Trade Atlas 1870-2013

Join us!

http://macfang.net

The Macfang workshop focuses on the role of space in complex networks. We bring exciting speakers from around the world to foster a leading collaborative view on the emergent field of Network Geometry. A number of topics will be covered, including but not limited to multiplex network geometry, geometric networks at criticality, emerging geometries of evolving networks, and the importance of space in processes such as disease propagation.

PhD open call, Network Science

We welcome applications for a three-year PhD position within our program of Complex Networks at UB. The gross annual pay is 16.400€ approx.. 

Eligibility Criteria

Candidates must have:

* a Master’s degree at the time of incorporation,

* a strong physics, mathematics and/or computer science background,

* a keen interest in developing and applying computational techniques to real systems from a Network Science perspective,

* an interest in working with real data,

* proved programming skills,

* fluency in spoken and written English.

To apply and for questions, you must send an email to Prof. M. Ángeles Serrano at marian.serrano@ub.edu indicating in the subject of the message “PhD-NS call “+ name surname of the candidate. The application package should include CV and a motivation letter. Selected candidates should be available for interviews (possibly via Skype) and practical tests.

Hidden geometric correlations in real multiplex networks

• Kaj-Kolja Kleineberg, Marián Boguñá, M. Ángeles Serrano & Fragkiskos Papadopoulos

Nature Physics 12, 1076–1081 (2016)

Real networks often form interacting parts of larger and more complex systems. Examples can be found in different domains, ranging from the Internet to structural and functional brain networks. Here, we show that these multiplex systems are not random combinations of single network layers. Instead, they are organized in specific ways dictated by hidden geometric correlations between the layers. We find that these correlations are significant in different real multiplexes, and form a key framework for answering many important questions. Specifically, we show that these geometric correlations facilitate the definition and detection of multidimensional communities, which are sets of nodes that are simultaneously similar in multiple layers. They also enable accurate trans-layer link prediction, meaning that connections in one layer can be predicted by observing the hidden geometric space of another layer. And they allow efficient targeted navigation in the multilayer system using only local knowledge, outperforming navigation in the single layers only if the geometric correlations are sufficiently strong.

Escaping the avalanche collapse in self-similar multiplexes

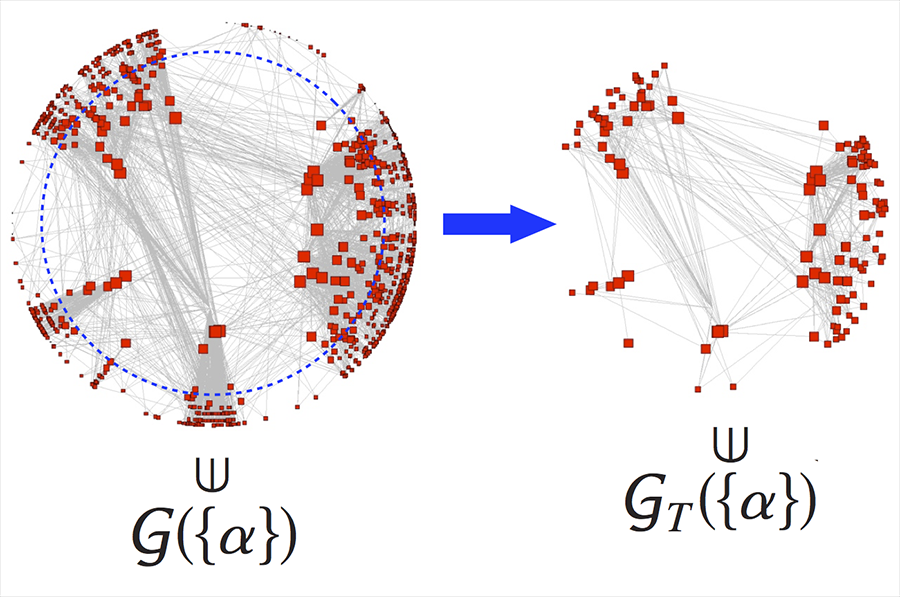
We deduce and discuss the implications of self-similarity for the robustness to failure of multiplexes, depending on interlayer degree correlations. First, we define self-similarity of multiplexes and we illustrate the concept in practice using the configuration model ensemble. Circumscribing robustness to survival of the mutually percolated state, we find a new explanation based on self-similarity both for the observed fragility of interconnected systems of networks and for their robustness to failure when interlayer degree correlations are present. Extending the self-similarity arguments, we show that interlayer degree correlations can change completely the global connectivity properties of self-similar multiplexes, so that they can even recover a zero percolation threshold and a continuous transition in the thermodynamic limit, qualitatively exhibiting thus the ordinary percolation properties of noninteracting networks. We confirm these results with numerical simulations.

Post-doctoral research associate position in complex networks at the University of Barcelona

MAPPING COMPLEXITY PROJECT

We invite applications for a Post-Doctoral Research Associate (1+1 years) in Network Science-Mapping Complexity at the University of Barcelona (Spain). The successful candidate will be required to join us in the investigation of complex networks embedded in hidden metric spaces to get insights into the connection between the structure and function in biological complex systems.

The position is funded by the grant "Mapping complexity: Embedding networks in hidden metric spaces" awarded by the James S. McDonnell Foundation 21st Century Science Initiative in Studying Complex Systems – Scholar Award, 2013.

We are seeking interested researchers with a PhD in Biological Sciences, Physics, Computer Science, or related fields, and proved computational/mathematical background. Experience in the investigations of Biological Systems is mandatory. We especially encourage women researchers to apply for the position.

Candidates can email a detailed CV together with an expression of interest to Dr. M. Ángeles Serrano, indicating "Mapping complexity PostDoc application" in the subject. Pre-selected candidates will be appointed for a personal interview and/or test assignments if necessary, and will be asked for one reference letter. Applications will be considered until the vacancy has been filled.

Contacts for any additional information:
Dr. M. Ángeles Serrano
Dr. Marián Boguñá

Regulation of burstiness by network-driven activation

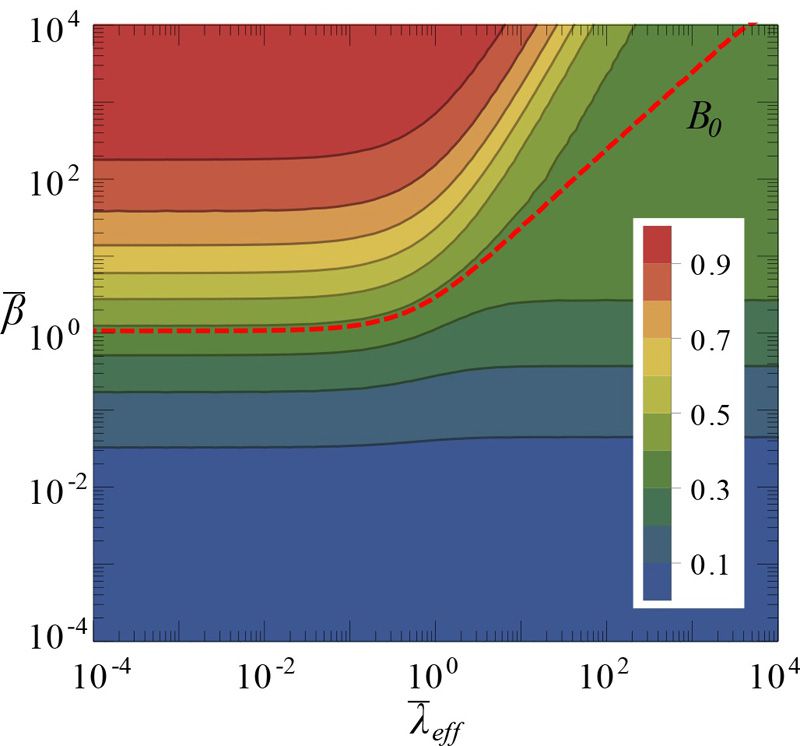
We prove that complex networks of interactions have the capacity to regulate and buffer unpredictable fluctuations in production events. We show that non-bursty network-driven activation dynamics can effectively regulate the level of burstiness in the production of nodes, which can be enhanced or reduced. Burstiness can be induced even when the endogenous inter-event time distribution of nodes’ production is non-bursty. We find that hubs tend to be less susceptible to the networked regulatory effects than low degree nodes. Our results have important implications for the analysis and engineering of bursty activity in a range of systems, from communication networks to transcription and translation of genes into proteins in cells.