The essence of complexity is summarized by the old aphorism coined out more than two thousand years ago: «The whole is more than the sum of its parts» (Lao Tse, Tao Te Ching, VI BC; Aristotle, Metaphysics, IV BC). Complex systems consist of a large number of components interacting in such a way that the group as a whole may produce nonlinear unexpected responses, often exhibiting phase transitions, cascades, crises, catastrophes, and other critical and extreme events.

The nature, intensity, and coupling of interactions among the different components encode these emerging intriguing features. Mapping complexity by tracing and appraising these interactions is now possible for many real systems, thanks to the amount of empirical data available and the current explosion in computing power. Through history, maps have been at the center of political, economic and geostrategic decisions to become a critical piece in our every day lives, serving as an integral, accurate, and relevant information source. Their appeal is not only visual, they provide a way of storing and presenting information and communicating findings, they let us recognize locational distributions and spatial relationships and make it possible for us to conceptualize patterns and processes that operate through space. Our goal is to map complexity, to map complex real systems in an embedding metric space that ought not to be geographical or spatially obvious, but that may be a condensate of different intrinsic attributes determining how distant, or conversely similar, the elements of the system are.

For discrete complex systems, such maps are based on topological objects called complex networks, graphs where elements are represented as nodes and their interactions as links, and on coarse-grained network representations that highlight their modular structure. All real networks are imprinted with universal features, regardless of their origin. One of the most paradigmatic examples is the small-world phenomenon, making every pair of nodes in a network to be connected in a short topological distance on average. As a consequence, small-world networks present an apparent lack of metric structure defined on the system. Certainly, in a small-world network, any pair of nodes is roughly separated by the same number of intermediate hops. This is the reason why complex networks are often considered as pure topological objects.

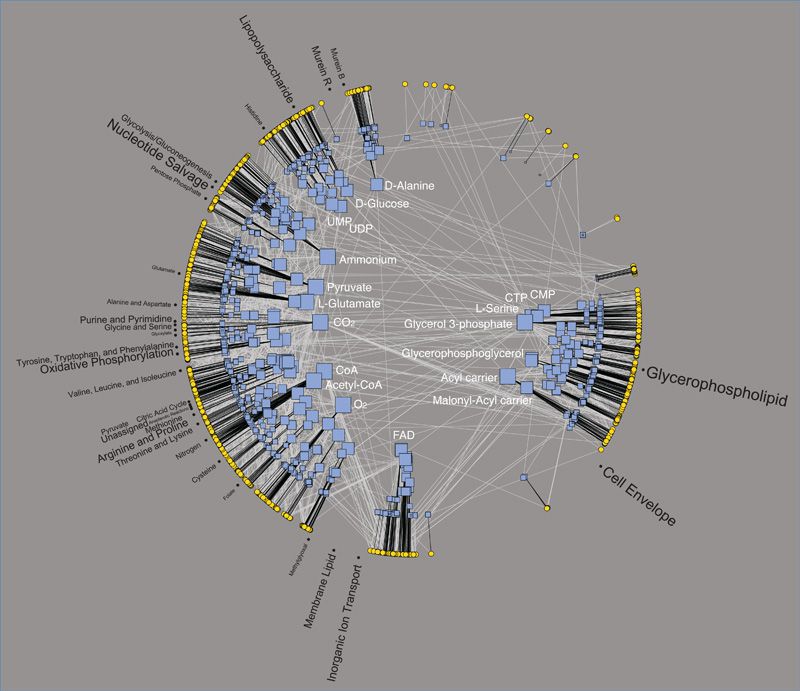
Yet, many networks are embedded in metric spaces. Some are explicit, like in airport networks, power grids, or urban networks, whereas some are hidden, like on the Internet or in economic networks. The discovery of such hidden metric spaces and the understanding of their role has become a major research area within the field of complex networks and promise to contribute significantly to the major challenges of the field, namely, the predictability, control, and engineering of complex systems. A germane example of the power of geometry in this context is our recent discovery of hidden metric spaces underlying both the Internet graph and metabolic networks. In the case of the Internet, such metric space provides a solution to the scalability limitations of current interdomain routing protocols. In the case of metabolic networks, it allows us to redefine the concept of biological pathways and to quantify their crosstalk.

Following this research, our proposal aims at developing the theoretical foundations of complex systems embedded in (hidden) metric spaces to get insights into the connection between the structure and function of complex systems. Elucidating this mysterious connection implies an impact far broader than the Internet or metabolic networks, including for recommendation systems, search engines, social dynamics, epidemic spreading, cancer and brain research, protein folding, and drug design. The proposed work will not only improve our knowledge of the basic principles of organization, function, and evolution of large-scale complex networks, but also transform research on how to model, predict, and control complex networked systems.